(Answered) Lesson 2 Homework – Statistical Methods

QUESTIONS

Question 1

Ages	Number of Students
15 – 18	2
19 – 22	4
23 – 26	8
27 – 30	9
31 – 34	6
35 – 38	3

Based on the frequency distribution above, is 22.5 a:

• Class midpoint
• Upper class limit
• Class width
• Class boundary
• Lower class limit

Question 2

Data was collected for 262 randomly selected 10 minute intervals. For each ten-minute interval, the number of people entering the atrium of a large mall were recorded. The data is summarized in the table below.

Number of Guests	Frequency
200 – 204	31
205 -209	74
210 – 214	38
215 – 219	31
220 – 224	88

What is the class width for this GTDT?

Class width =

Question 3

Here is a data set that has a nearly normal distribution.

Data	Data	Data	Data
57.84	51.97	39.51	44.7
41.55	37.73	68.84	61.61
48.25	73.63	37.52	62.53
57.68	56.08	54.7	50.72
50.83	44.81	58.13	59.02
44.44	65.56	42.92	51.2
48.84	53.21	45.72	48.06
60.63	42.98	57.59	45.89
42.54	44.14	36.24	60
30.85	57.93	36.39	65

In building a GFDT for this data set, you need to know how many values are in the class from 60 to 65. You decided that each class will include the lower class limit, but not the upper class limit. So, how many values are there in the interval [60,65)?

Frequency =

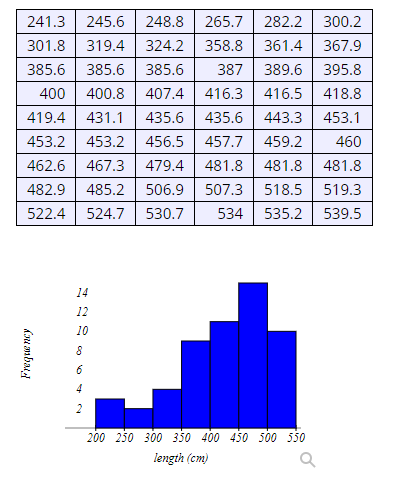
Question 4

Data was collected for 300 fish from the North Atlantic. The length of the fish (in mm) is summarized in the GFDT below.

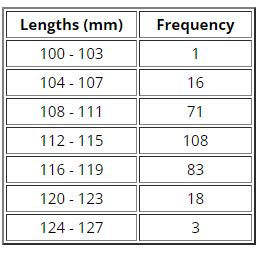
What is the class midpoint for the first class?

Class midpoint =

Question 5

Data was collected for 300 fish from the North Atlantic. The length of the fish (in mm) is summarized in the GFDT below.

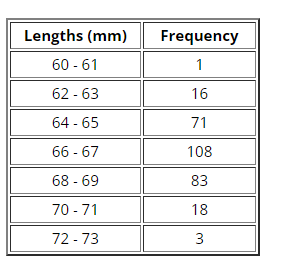
What is the class boundary between the fourth and fifth classes?

Class boundary =

Question 6

Data was collected for 300 fish from the North Atlantic. The length of the fish (in mm) is summarized in the GFDT below.

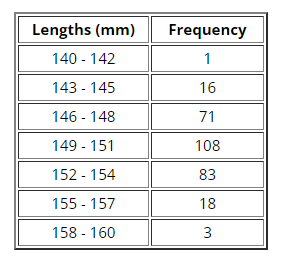
What is the lower class boundary for the first class?

Class boundary =

Question 7

Here is a data set:

15	69	36	72
134	136	83	207
72	43	95	205
88	109	101	66
162	142	247	133
84	80	187	137
82	56	4	88

The goal is to construct a grouped frequency distribution table (GFDT) for this data set. The GFDT should have 10 classes with a “nice” class width. Each class should contain its lower class limit and each sequential lower class limit should increase by increments of the class width.
This problem is to determine what the class width should be.
What is the range of this data set?

Range =

Using this information, if the goal is to have 10 classes, what is the nicest class width?
optimal class width =

Question 8

Here is a data set:

696	440	655	363
678	566	469	655
496	565	473	389
488	654	363	462
574	615	560	470
572	528	441	847
463	408	501	366

The goal is to construct a grouped frequency distribution table (GFDT) for this data set. The GFDT should have 10 classes with a “nice” class width. Each class should contain its lower class limit and each sequential lower class limit should increase by increments of the class width. It has been determined that the ideal class width would be 50.

This problem is to determine what the first lower class limit should be.
What is the minimum of this data set?

Min =

What is the minimum divided by the class width?
minimum ÷ class width =

This number rounds down to what integer =

Using this value, if the goal is to have a lower class limits that are multiples of the class width, what should be the first lower class limit?
1st lower class limit =

Question 9

2540	2680	2880	4120
3480	3050	3740	3060
2950	3370	3020	3160
3290	3000	3560	3590
3330	4270	2540	3620
4710	3170	3800	2820
2270	3610	3070	4300

Construct a grouped frequency distribution table (GFDT) for this data set. You want 10 classes with a “nice” class width. Your classes should be labeled using interval notation. Each class should contain its lower class limit and each sequential lower class limit should increase by increments of the class width. In that the data appears to be discrete, use a closed-interval to label each class.

Data Range	Frequency
2250, 2490
2500,2740
2750,2990
3000,3240
3250,3490
3500, 3740
3750,3990
4000,4240
4250,4490
4500,4740

Question 10

The following data represents the age of 30 lottery winners.

20	26	26	27	34	35
36	36	37	38	39	40
43	48	49	49	56	59
60	62	64	68	70	72
73	74	74	74	77	87

Complete the frequency distribution for the data.

Age	Frequency
20-29
30-39
40-49
50-59
60-69
70-79
80 -89

Question 11

An ungrouped frequency distribution table (FDT) works for which levels of measurements?

• Ratio
• Interval
• Ordinal
• Nominal

Question 12

In SPSS, if a value falls on an upper/lower real limit, then it is always assigned to the lower interval.

• True
• False

Question 13

One indicator that you’ve done your computations correctly for a cumulative (G)FDT is that the _______ category should have a cumulative frequency value equal to the sample size.

Fill in the blank: ________

Question 14

For GFDTs and the relative GFDTs, the points are centered above the class midpoint.  For cumulative or relative cumulative GFDTs, the points are drawn above the _______ interval limits.
Fill in the blank: ___________

Question 15

The line graph below shows the number of times Maria drove her car each day of the week.

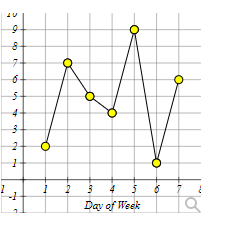
How many times did Maria drive her car on day 4?

Question 16

Kara categorized her spending for this month into four categories: Rent, Food, Fun, and Other. The amounts she spent in each category are pictured here.

How much total money did Kara spend this month?

Question 17

Kara categorized her spending for this month into four categories: Rent, Food, Fun, and Other. The amounts she spent in each category are pictured here.

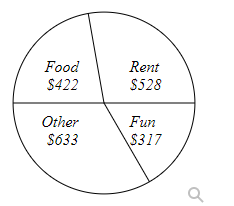
What percent of her total spending did she spend on Rent? Answer to the nearest whole percent.

Question 18

Kiara categorized her spending for this month into four categories: Rent, Food, Fun, and Other. The percents she spent in each category are pictured here.

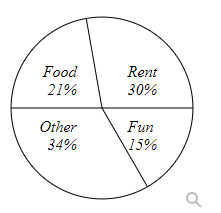
If Kiara spent a total of $2900 this month, how much did she spend on Rent?

Question 19

Elena categorized her spending for this month into four categories: Rent, Food, Fun, and Other. The percents she spent in each category are pictured here.

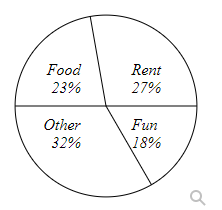
If Elena spent a total of $2400 this month, how much did she spend on Fun?

• $18
• $432
• $456

Question 20

Determine the distribution of the data pictured below

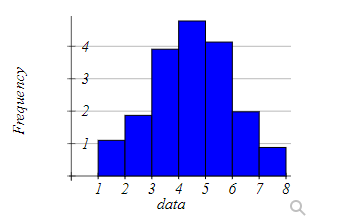
• Uniform
• Bell-shaped
• Skewed-right
• Skewed-right

Question 21

Determine the distribution of the data pictured below.

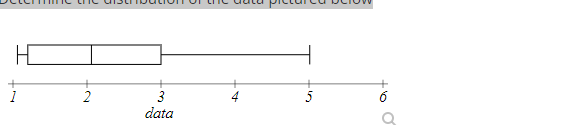
• Uniform
• Bell-shaped
• Skewed-right
• Skewed-left

Question 22

The line graph below shows the number of times Maria drove her car each day of the week.

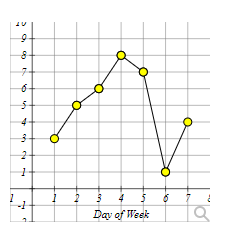
How many times did Maria drive her car on day 4?

Question 23

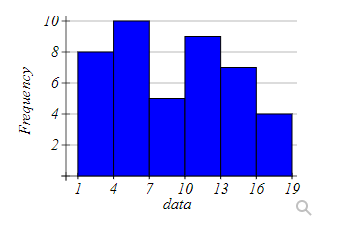
Based on the histogram above, what is the class width?

Class width =

What is the sample size?

Sample size =

Question 24

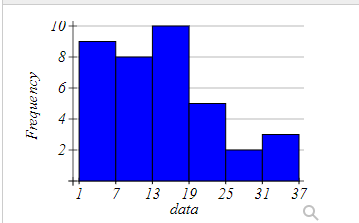
Based on the histogram above, what is the frequency of the class containing the value 26.

Question 25

Given two paired quantitative data sets, choose the best type of graph to represent the data.

• Pareto chart
• Scatter plot
• Ogive
• Histogram

Question 26

Determine the distribution of the data pictured below.

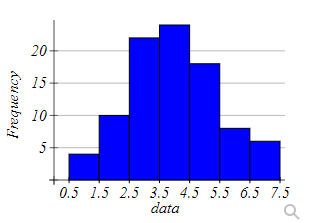
• Uniform
• Bell-shaped
• Skewed-right
• Skewed-left.

Question 27.

The data in the figure below represents the number of stars earned by 140 performers in a talent competition.

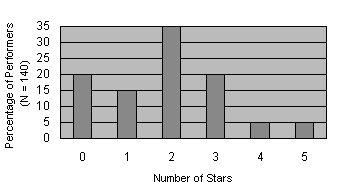
How many performers earned exactly 5 stars? (be careful – compare the question wording to the scale on the graph).

Question 28.

Identify the histogram for the frequency distribution below.

Bin	Frequency
[2,7)	2
[7,12)	5
[12,17)	5
[17,22)	3
[22,27)	2

Question 29

Barb recorded the color of cars in the town parking lot. She summarized the data in the bar chart below:

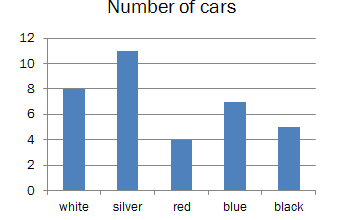
How many of the cars were white?

Question 30

The population of a small village is shown below.

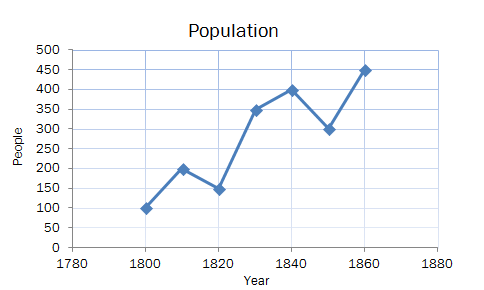
What was the population in 1810?

Question 31

The population of a small village is shown below.

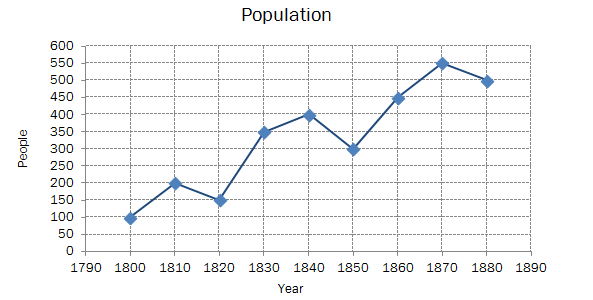
What was the population in 1880?

Question 32

The following data represents the age of 30 lottery winners.

21	25	27	28	28	31
33	37	37	38	38	39
40	48	49	50	55	62
64	70	71	72	72	72
73	74	75	76	76	84

Complete the frequency distribution for the data.

Bin	Frequency
20-29
30-39
40-49
50-59
60-69
70-79
80-89

Question 33

The inter-quartile range is obtained from subtracting the _________ hinge from the ___________hinge.

Question 34

Data that lie beyond the fences are possible _______

Question 35

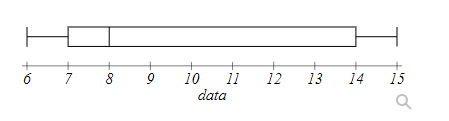
Based on the boxplots above, identify the 5 number summary.

Answer: ____, ___ , ___ , ___ , ___ .

Question 36.

Find the minimum for this list of the numbers.

88	1
27	72
71	6
95	50
53	69
11	94
49	30
92

Minimum =

Question 37

Find the first quartile for the list of numbers

22	62
35	65
91	98
59	60
30	13
40	75
14	29
86

Quartile =

Question 38

Find the third quartile for this list of numbers

35	62
85	19
76	55
36	74
82	9
80	67
18	83
95

Quartile 3 =

Question 39

Find the maximum for this list of numbers.

36	19
48	51
15	39
66	72
92	100
52	3
54	42
50

Maximum =

Question 40

Based on the boxplot above, what is the value for the Q1.

Question 41

Here is a sample data set.

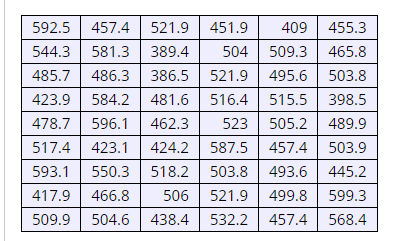
Find the first quartile for this data set.

Q1 =

Find the third quartile for this data set.

Q3 =

Find the interquartile range for this data set.

IQR=

Question 42

Here is a sample data set.

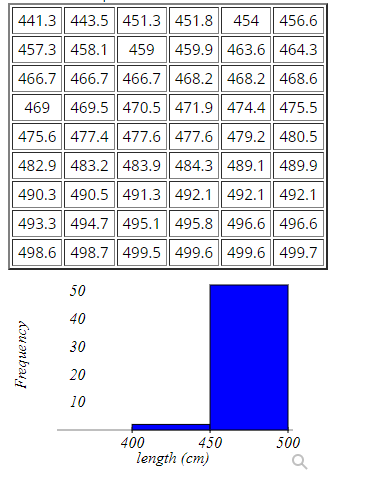
Find the minimum for this data set.

Min =

Find the first quartile for this data set.

Q1 =

Find the median for this data set.

Median =

Find the third quartile for this data set.

Q3 =

Find the maximum for this data set.

Max =

Question 43

Here is a sample data set.

Find the first quartile for this data set.

Q1 =

Find the third quartile for this data set.

Q3 =

Find the interquartile range for this data set.

IQR =

Find the lower fence separating outliers from usual values.

Fence low =

Find the upper fence separating outliers from usual values.

Fence high =

Question 44

Find the first and third quartile for the data shown.

X
1.1
2
6.5
7.6
10
14.7
16.9
17.5
23.7
27.1

Q1=

Q3 =

Question 45

The boxplot below shows salaries for Construction workers and Teachers.

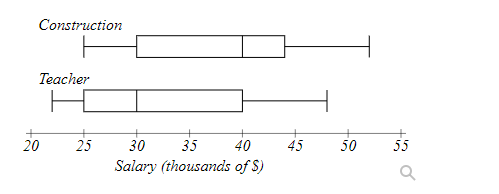
Jennie makes the minimum salary for a construction worker. Markos makes the median salary for a teacher.
Who makes more money?

• Jennie
• Markos

How much more?

Question 46

The boxplot below shows salaries for CPAs and Actuaries in a town.

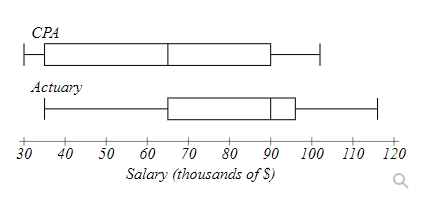
If a person is making the median salary for a CPA, they are making less than ________ of Actuaries.

Question 47

The boxplot below shows salaries for Actuaries and CPAs.

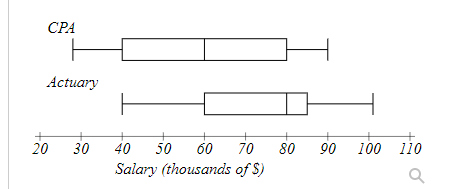
Ben makes the median salary for an Actuary. Bella makes the first quartile salary for a CPA.
Who makes more money?

• Bella
• Ben

How much more?

Question 48.

The boxplot below shows salaries for Construction workers and Receptionists.

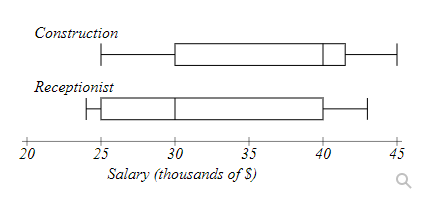
Jennie makes the minimum salary for a construction worker. Markos makes the median salary for a receptionist.

Who makes more money?

• The construction worker
• The receptionist
• They make the same amount.

Question 49

Here is a sample data set (n=48) that is nearly normal (as can be seen in the histogram provided after the data set).

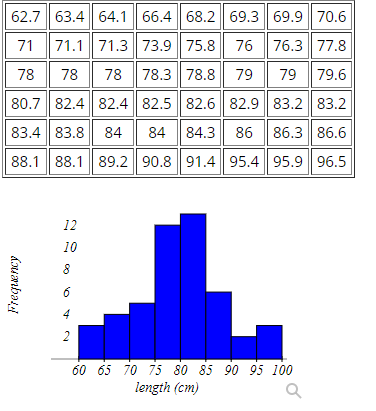
How many mild outliers are in this data set?

Answer =

How many extreme outliers are in this data set?

Answer =

Question 50

Here is a sample data set (n=48) that is nearly normal (as can be seen in the histogram provided after the data set).

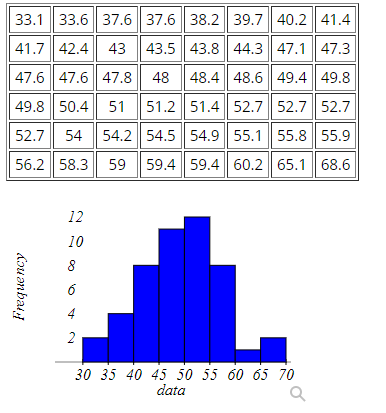
How many outliers are in this data set?

Question 51 Here is a sample data set (n=48) that is nearly normal with two outliers (as can be seen in the histogram provided after the data set).

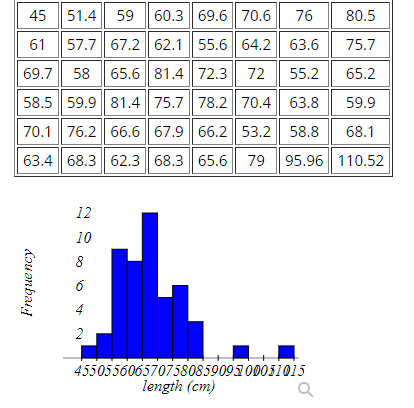
How many mild outliers are in this data set?

How many extreme outliers are in this data set?

Question 52

Choose the correct label the point on the boxplot represented by the question mark:

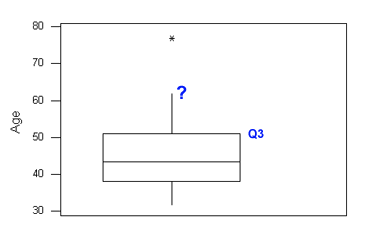
Q1

Q3

M

Min

Max

IQR

Range

None of the above

Question 53

Choose the correct label for the point on the boxplot represented by the question mark:

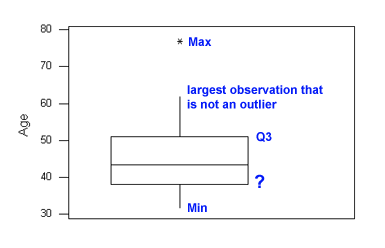
Q1

Q3

M

Min

Max

IQR

Range

None of the above

Question 55

Choose the correct label for the point on the boxplot represented by the question mark:

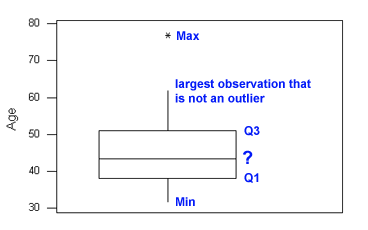
Q1

Q3

M

Min

Max

IQR

Range

None of the above

Question 56

Choose the correct label for the element (in red) on the boxplot represented by the question mark:

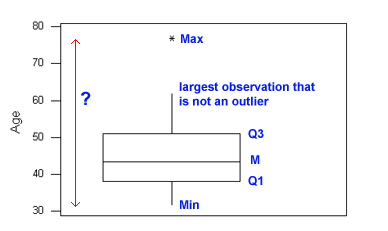
Q1

Q3

M

Min

Max

IQR

Range

None of the above

Question 57

Choose the correct label for the element (in red) on the boxplot represented by the question mark:

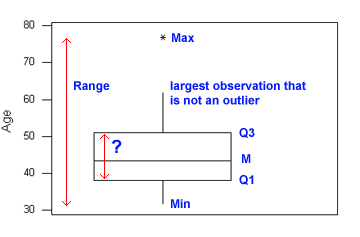
Q1

Q3

M

Min

Max

IQR

Range

None of the above.

ANSWERS

Question 1

Ages	Number of Students
15 – 18	2
19 – 22	4
23 – 26	8
27 – 30	9
31 – 34	6
35 – 38	3

Based on the frequency distribution above, is 22.5 a:

• Class midpoint
• Upper class limit
• Class width
• Class boundary
• Lower class limit

To access all answers (100% correct), use the purchase button below.

$40.00 – Purchase Checkout Added to cart