QUESTIONS
Question 1
A simple random sample of size n=10 is obtained from a population that is normally distributed with a mean of 40 and a standard deviation of 3. Is the sampling distribution normally distributed? Why?
- Yes, the sampling distribution is normally distributed because the population is normally distributed.
- Yes, the sampling distribution is normally distributed because the population mean is greater than 30.
- No, the sampling distribution is not normally distributed because the population is not normally distributed.
- No, the sampling distribution is not normally distributed because the sample size is less than 30.
Question 2
Which of the following is true about sampling distributions?
- Sampling distributions get closer to normality as the sample size increases.
- Sampling distribution of the mean is always right skewed since means cannot be smaller than 0.
- Shape of the sampling distribution is always the same shape as the population distribution, no matter what the sample size is.
- Sampling distributions are always nearly normal.
Question 3
Which of the following statements are true?
- It is okay to use the median to estimate the mean since both are a measure of the center of a distribution.
- It is okay to use the standard deviation to estimate the IQR since both are measures of variability.
- Point estimates based on a sample are sometimes far from a parameter’s value
- i only
- ii only
- iii only
- i and ii
- i and iii
- i, ii, and iii
Question 4
Suppose that the efficacy of a certain drug is 0.4. Consider the sampling distribution (sample size n = 212) for the proportion of patients cured by this drug.
What is the mean of this distribution? _______
What is the standard error of this distribution?
Question 5
A 2011 Gallup survey based on telephone and face-to-face interviews with 4,220 adults in China, aged 15 and older suggests that 30% smoke regularly or occasionally. The following is also noted “one can say with 95% confidence that the maximum margin of sampling error is 2.2 percentage points”. Which of the following is true based on the results of this survey?
- We are 95% confident that 27.8% to 32.2% of all Chinese adult smoke
- We are 95% confident that 25.6% to 34.4% of all Chinese adult smoke.
- Exactly 30% of all Chinese adults smoke
- If the sample size was larger, the margin of error would be larger as well.
- If we were to randomly sample another group of 4,220 Chinese adults we would find that exactly 30% of them smoke as well.
Question 6
SAT scores are distributed with a mean of 1,500 and a standard deviation of 300. You are interested in estimating the average SAT score of first year students at your college. If you would like to limit the margin of error of your 95% confidence interval to 25 points, how many students should you sample?
Give a whole number answer.
Question 7
A random sample of 75 students at the University of Minnesota spend an average of $614 per month in rent with a standard deviation of $219. The distribution is moderately skewed to the high end. Which of the following statements are true?
- 95% of students at the university spend $564 to $664 on rent.
- We are 95% confident that the average rent for students at the university is between $564 and $664.
- Because we cannot examine other characteristics of the students in the random sample, it is not advisable to construct a confidence interval.
- i only
- ii only
- iii only
- i and ii
- i, ii, and iii
Question 8
Which of the following is false about the margin of error of a confidence interval?
- As confidence level increases, margin of error increases as well
- As standard deviation of the sample increases, margin of error increases as well.
- As sample size increases, margin of error increases as well.
Question 9
Below is a hypothesis test set up by a student who recently took introductory statistics:
H0: x = 5
HA: x ≠ 5
The sample mean of 100 cases used to implement the hypothesis test is x = 4.2. Which of the following statements are accurate?
- This is a one-sided hypothesis test.
- There is an error in how these hypotheses were constructed.
- It would be reasonable to swap “<” for “≠” in the alternative hypothesis.
- i only
- ii only
- iii only
- i and ii
- i and iii
- i, ii, and iii
Question 10
Express the confidence interval 45.8%±5%45.8%±5% in interval form.
Express the answer in decimal format.
Question 11
Match each step on the left with the procedure at that step on the right.
| STEP | TODO |
| _____ | Write claim symbolically |
| _____ | Compare p-value to alpha |
| _____ | Write conclusion |
| _____ | Reject or fail to reject null |
| _____ | Calculate p-value |
| _____ | Identify test type and distribution to use |
| _____ | Write null and alternate hypothesis |
| ____ | Calculate sample statistics |
Question 12
A random sample of 100 US cities yields a 90% confidence interval for the average annual precipitation in the US of 33 inches to 39 inches. Which of the following is false based on this interval?
- The sample average is 36 inches.
- 90% of random samples of size 100 will have sample means between 33 and 39 inches.
- We are 90% confident that the average annual precipitation in the US is between 33 and 39 inches.
- The margin of error is 3 inches.
Question 13
Test the claim that the proportion of men who own cats is smaller than -2% at the .10 significance level.
The null and alternative hypothesis would be:
- H0: p = – 0.02, H1: p > – 0.02
- H0: u = -0.02, H1: u ≠ – 0.02
- H0: u = -0.02, H1: u > – 0.02
- H0: u = -0.02, H1: u < – 0.02
- H0: p = -0.02, H1: p ≠ – 0.02
- H0: p = -0.02, H1: p < – 0.02
The test is:
- Right-tailed
- Two-tailed
- Left-tailed
Based on a sample of 80 people, 7.5% owned cats.
The p-value is (to 2 decimals) ______
Based on this, we:
- Fail to reject the null hypothesis
- Reject the null hypothesis
Question 14
A professor using an open-source introductory statistics book predicts that 60% of the students will purchase a hard copy of the book, 25% will print it out from the web, and 15% will read it online. At the end of the semester she asks her students to complete a survey where they indicate what format of the book they used. Of the 126 students, 71 said they bought a hard copy of the book, 30 said they printed it out from the web, and 25 said they read it online. What would be the appropriate set of hypotheses for testing if the professor’s predictions were accurate?
- H0: The actual proportion of students who purchase the hard copy of the book is 60%. HA: The actual proportion of students who purchase the hard copy of the book is higher than 60%.
- H0: The distribution of the format of the book used by the students follows the professor’s predictions. HA: The distribution of the format of the book used by the students does not follow the professor’s predictions.
- H0: The distribution of the format of the book used by the students does not follow the professor’s predictions. HA: The distribution of the format of the book used by the students follows the professor’s predictions.
- H0: The actual proportion of students who purchase the hard copy of the book is higher than 60%. HA: The actual proportion of students who purchase the hard copy of the book is lower than 60%.
Question 15
Rock-paper-scissors is a hand game played by two or more people where players choose to sign either rock, paper, or scissors; with their hands. We would like to test if players choose between these three options randomly, or if certain options are favored above others. What hypothesis test should we conduct to answer this research question?
- Compare two proportions.
- Chi square test of independence.
- Chi square test of goodness of fit.
- Compare two means.
Question 16
Here is a scatter plot for a set of bivariate data. What would you estimate the correlation coefficient to be?
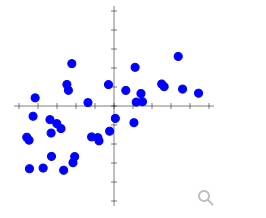
- -0.9
- -0.6
- 0
- 0.6
- 0.9
Question 17
Which of the following is false?
- Correlation measures the strength of linear association between two numerical variables.
- Correlation coefficient and the slope always have the same sign (positive or negative).
- If the correlation between two variables is close to 0.01, then there is a very weak linear relation between them.
- If the correlation coefficient is 1, then the slope must be 1 as well.
ANSWERS
Question 1
A simple random sample of size n=10 is obtained from a population that is normally distributed with a mean of 40 and a standard deviation of 3. Is the sampling distribution normally distributed? Why?
- Yes, the sampling distribution is normally distributed because the population is normally distributed.
- Yes, the sampling distribution is normally distributed because the population mean is greater than 30.
- No, the sampling distribution is not normally distributed because the population is not normally distributed.
- No, the sampling distribution is not normally distributed because the sample size is less than 30.
To access all answers, use the purchase button below.
